tree in data structure | data structure and algorithm | insertion, search, pre-order, in-order, post-order

Trees in data structure

Definition of tree:

Trees is define as, it is non linear data structure consist of two child and one root.

Both child are:

1. Left child

2. Right child

Because in tree every node of tree has at least two child.

Tree is abstract data type which is used for data storage.

Benefits of tree:

Binary tree has many benefits some of these are explain below:

Searching purpose are more fast on tree as compared to link list

Insertion and deletion also fast in tree as compared to link list.

 

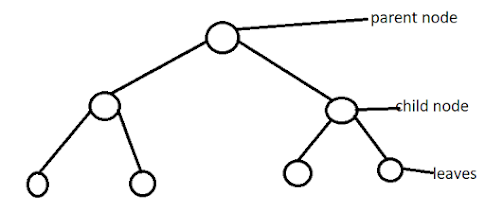
Parts of tree:

There are many parts of tree:

Root:

Root is starting point of every tree which is intial point of every tree. 

Node:

Node is parent of every leaves and every node has siblings.

Leaves:

Leaves are child of node.

Sub tree:

Every tree has sub tree.

Child:

Chide is below the node of every parent node which are connected by edges and edges link one node to another node.

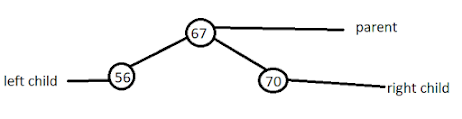
Rules of tree:

1. Left child of every of tree has less value then the parent value.

2. Right child of every tree has always greater value then parent value. 

Code of the tree:

#include<iostream>
#include<conio.h>
using namespace std;
class tree
{
	private:
	struct node
	{
		int data;
		node *left;
		node *right;	
	};
	public:
	node *root = NULL;
	void insert(int &n);
	void search();
	void preorder(node *ptr);
	void inorder(node *ptr);
	void postorder(node *ptr);
	void del();	
};
	void tree::insert(int &n)
	{
		node *new_node = new node;
		new_node -> data = n;
		new_node -> left = NULL;
		new_node -> right = NULL;
		if(root == NULL)
		{
			root = new_node;
			cout<<"\n\n "<<n<<" Value Inserted Successfully...";
		}
		else
		{
			node *ptr = root;
			node *pre = NULL;
			while(ptr != NULL)
			{
				if(n > ptr -> data)
				{
					pre = ptr;
					ptr = ptr -> right;
					if(ptr == NULL)
					{
					pre -> right = new_node;
					cout<<"\n\n "<<n<<" Value Inserted Successfully...";
					}
				}
				else if(n < ptr -> data)
				{
					pre = ptr;
					ptr = ptr -> left;
					if(ptr == NULL)
					{
					pre -> left = new_node;
					cout<<"\n\n "<<n<<" Value Inserted Successfully..."; 
					}
				}
				else
				{
					cout<<"\n\n "<<n<<" Value is Duplicated...";
					delete new_node;
					break;
				}
			}
		}
	}
	void tree::search()
	{
		system("cls");
		int n,found=0;
		cout<<"\n\n\t\t\t\t Search Record";
		if(root == NULL)
		cout<<"\n\n Tree is Empty...";
		else
		{
			cout<<"\n\n Enter Value : ";
			cin>>n;
			node *ptr= root;
			while(ptr != NULL)
			{
				if(n == ptr -> data)
				{
					cout<<"\n\n "<<n<<" Value is Found...";
					found++;
					break;
				}
				else if(n > ptr -> data)
				{
					ptr = ptr -> right;
				}
				else
				{
					ptr = ptr -> left;
				}
			}
			if(found == 0)
			cout<<"\n\n "<<n<<" Value Can't Found...";
		}
	}
	void tree::preorder(node *ptr)
	{
		if(root == NULL)
		cout<<"\n\n Tree is Empty...";
		else
		{
			if(ptr != NULL)
			{
				cout<<"\n "<<ptr -> data;
				preorder(ptr -> left);
				preorder(ptr -> right);
			}
		}
	}
	void tree::inorder(node *ptr)
	{
		if(root == NULL)
		cout<<"\n\n Tree is Empty...";
		else
		{
			if(ptr != NULL)
			{
				inorder(ptr -> left);
				cout<<"\n "<<ptr -> data;
				inorder(ptr -> right);
			}
		}
	}
	void tree::postorder(node *ptr)
	{
		if(root == NULL)
		cout<<"\n\n Tree is Empty...";
		else
		{
			if(ptr != NULL)
			{
				postorder(ptr -> left);
				postorder(ptr -> right);
				cout<<"\n "<<ptr -> data;
			}
		}
	}

main()
{
	tree t;
	int choice,n;
	p:
	system("cls");
	cout<<"\n\n 1. Insert Record";
	cout<<"\n 2. Search Record";
	cout<<"\n 3. Pre Order Traversal";
	cout<<"\n 4. In Order Traversal";
	cout<<"\n 5. Post Order Traversal";
	cout<<"\n\n Your Choice : ";
	cin>>choice;
	switch(choice)
	{
		case 1:
			system("cls");
			cout<<"\n\n\tInsert Record";
			cout<<"\n\n Enter Value : ";
			cin>>n;
			t.insert(n);
			break;
		case 2:
			t.search();
			break;
		case 3:
			system("cls");
			t.preorder(t.root);
			break;
		case 4:
			system("cls");
			t.inorder(t.root);
			break;
		case 5:
			system("cls");
			t.postorder(t.root);
			
			break;
		case 6:
			exit(0);
		default:
			cout<<"\n\n Invalid Value...!";
	}
	goto p;
}